2回にわけてミニマムに遊べるテトリス風の落ちものパズルゲームを作っていきます。ゲームエンジンやライブラリを使わずに、素のHTMLとJavaScriptだけでゲームを作ります。
以下のような人のためにあります。
ゲームを作ってみたいけど、何をどうしていいか分からない。
単純なゲームを作りたいだけなのに、UnityとかUnreal Engineは面倒くさい。
ある程度プログラミングの知識がある人を対象にしています。
テトリスとは何か?
テトリスは1980年代末から1990年代に流行した、元祖落ちゲーのパズルゲームです。詳しくはWikipediaをご覧ください。

この記事で作るもの
テトリスのゲーム要素を構成する要素のうち、
ブロックが落ちる、積み上がる、横いっぱいに積まれたら行が消える。を実装します。
カーソルの左右キーを押してブロックを動かしてみてください。
‘d’で落ちるスピードが速くなり、’r’で最初からやり直します。
先に読んでおくもの
この記事では、以下のゲームの基本構成技術の説明は省きます。
- 画面上に絵を描画する方法
- ユーザのキー入力を受け付ける方法
- ゲームの状態管理の方法
これらは、以下の記事で説明していますので、詳細を知りたい方は読んでみてください。
ソースコード
<html>
<center>
<canvas id="gameCanvas" width="240" height="440" style="border:1px solid #000000; background-color: #000;"></canvas>
<script type="text/javascript" src="index.js"></script>
</html>const canvas = document.getElementById('gameCanvas');
const context = canvas.getContext('2d');
const SCREEN_W = 10
const SCREEN_H = 20
const BLOCK_SIZE = 20
let screen = Array(SCREEN_H*SCREEN_W);
// ブロック
let blockX = 5;
let blockY = 0;
const blockShape = [1,1,0,0,
1,1,0,0]
// 入力ハンドラー
document.addEventListener('keydown', keyDownHandler, false);
function keyDownHandler(event) {
if (event.key === 'Left' || event.key === 'ArrowLeft') {
if (!outOfArea(blockX-1, blockY, blockShape)
&& !blockHit(blockX-1, blockY, blockShape))
blockX -= 1;
}
if (event.key === 'Right' || event.key === 'ArrowRight') {
if (!outOfArea(blockX+1, blockY, blockShape)
&& !blockHit(blockX+1, blockY, blockShape))
blockX += 1;
}
if (event.key === 'd') {
if (!outOfArea(blockX, blockY+1, blockShape)
&& !blockHit(blockX, blockY+1, blockShape))
blockY += 1;
}
if (event.key == 'r') {
init();
}
}
function drawRect(x,y, block) {
context.strokeStyle = '#fff';
context.lineWidth = 2;
context.strokeRect((x+1) * BLOCK_SIZE, (y+1) * BLOCK_SIZE, BLOCK_SIZE, BLOCK_SIZE);
if (block==1) {
context.fillStyle = '#fff'
context.fillRect((x+1) * BLOCK_SIZE, (y+1) * BLOCK_SIZE, BLOCK_SIZE, BLOCK_SIZE);
}
}
function drawScreen() {
for (j = 0; j < SCREEN_H; j++) {
for (i = 0; i < SCREEN_W; i++) {
block = screen[ i + j*SCREEN_W ];
drawRect(i, j, block);
}
}
}
function hasBrick(x,y) {
return 0!=screen[x + y*SCREEN_W];
}
function doFuncOnShape(shape, f) {
if (shape == undefined) return;
for (j = 0; j < 2; j++) {
for (i = 0; i < 4; i++) {
if (shape[i+j*4]==1) {
f(i, j)
}
}
}
}
function outOfArea(x, y, shape) {
let flg = false;
doFuncOnShape(shape, function (i,j) {
if (x+i < 0 || x+i >= SCREEN_W || y+i >= SCREEN_H)
flg = true;
});
return flg;
}
function drawBlock(x, y, shape) {
doFuncOnShape(shape, function (i,j) {
drawRect(x+i, y+j, 1);
});
}
function blockHit(x, y, shape) {
// ブロックの形データ4 x 2を見ていく
for (j = 0; j < 2; j++) {
for (i = 0; i < 4; i++) {
if (shape[i+j*4]==1) {
if (hasBrick(x+i, y+j))
return true;
}
}
}
return false;
}
function putBlock(x, y, shape) {
// ブロックの形データ4 x 2を見ていく
for (j = 0; j < 2; j++) {
for (i = 0; i < 4; i++) {
if (shape[i+j*4]==1) {
setBrick(x+i, y+j, 1);
}
}
}
}
function setBrick(x, y, block) {
screen[x + y*SCREEN_W] = block;
}
function lineIsComplete(line) {
for (i = 0; i < SCREEN_W; i++) {
if (screen[i + line*SCREEN_W]==0)
return false;
}
return true;
}
function checkLineComplete() {
do {
deleted_line = false;
for (j = SCREEN_H-1; j >=0 ; j--) {
if (lineIsComplete(j)) {
deleteLine(j);
j++;
deleted_line = true;
}
}
} while (deleted_line);
}
function deleteLine(line) {
for (j = line-1; j >= 0; j--) {
copyLine(j,j+1);
}
}
function copyLine(src, tgt) {
for (i = 0; i < SCREEN_W; i++) {
screen[i + tgt*SCREEN_W] = screen[i + src*SCREEN_W];
}
}
const WAIT_COUNT = 40;
let wait_count = 0;
function is_in_interval(count) {
wait_count += 1;
if (wait_count < count) {
return true;
}
wait_count = 0;
return false;
}
function update() {
if (is_in_interval(WAIT_COUNT))
return;
if (blockHit(blockX, blockY+1, blockShape)) {
putBlock(blockX, blockY, blockShape); // ブロックを積み上げる
blockY = 0;
return;
}
checkLineComplete();
blockY += 1;
}
function draw_text_center(text, font='30px Consolas') {
context.font = font;
context.textAlign = 'left';
text_w = context.measureText(text).width;
context.fillText(text, canvas.width/2-text_w/2, canvas.height/2);
}
function init() {
screen.fill(0);
}
function draw() {
context.clearRect(0, 0, canvas.width, canvas.height);
drawScreen();
drawBlock(blockX, blockY, blockShape);
update();
}
init();
setInterval(draw, 10);
画面の構成
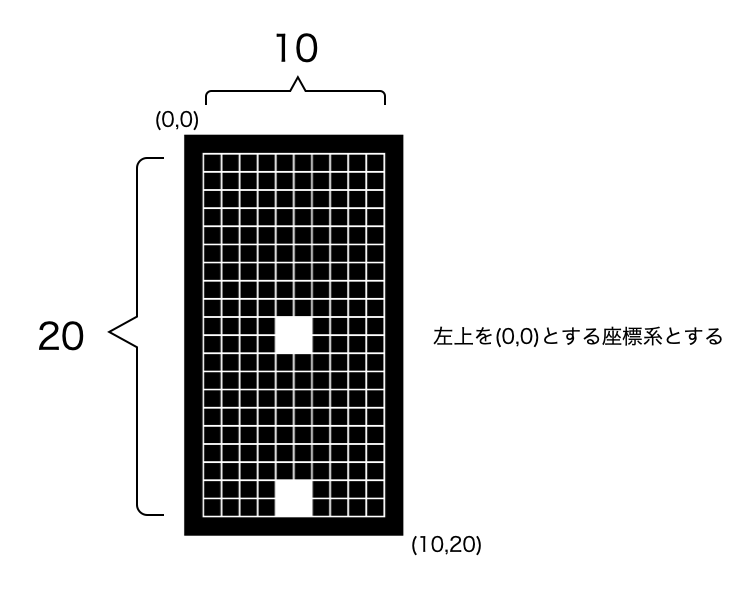
このゲームの画面は横10 x 縦20の区画で構成します。
各区画にブロックが存在するかどうかを管理するバッファとして、10 x 20の一次元配列を用意します。
screenの定義
const SCREEN_W = 10
const SCREEN_H = 20
・・・
let screen = Array(SCREEN_H * SCREEN_W);配列に入れるデータは0と1です。0は空白、1はブロックがあることを意味します。例えば、2列3行目のマスにブロックを入れたい場合は、以下の実装になります。
screen[ 2 + 3 * SCREEN_W ] = 1; // (2列, 3行)目にブロックを入れるこのscreen全体の描画は以下のコードでやっています。
function drawScreen() {
for (j = 0; j < SCREEN_H; j++) {
for (i = 0; i < SCREEN_W; i++) {
block = screen[ i + j*SCREEN_W ];
drawBrick(i, j, block);
}
}
}一行目から要素を順に取り出していって、drawRect()で矩形を描画しています。
function drawRect(x,y, block) {
context.strokeStyle = '#fff';
context.lineWidth = 2;
context.strokeRect((x+1) * BLOCK_SIZE, (y+1) * BLOCK_SIZE, BLOCK_SIZE, BLOCK_SIZE);
if (block==1) {
context.fillStyle = '#fff'
context.fillRect((x+1) * BLOCK_SIZE, (y+1) * BLOCK_SIZE, BLOCK_SIZE, BLOCK_SIZE);
}
}blockが0なら黒抜きの矩形、1ならブロックが存在するので白塗りの矩形を描画します。
落ちるブロックと当たり判定
落ちるブロックを実現するには位置情報が必要です。以下の変数です。
let blockX = 5;
let blockY = 0;10 x 20のscreenの中の座標として管理します。Xは列数、Yは行数です。
また、落ちる際に当たり判定には、ブロックの形も重要です。このデモではブロックは 2 x 2のマスを使う四角形のものを用意しました。この形を表すデータ構造は下記です。
const blockShape = [1,1,0,0,
1,1,0,0]このデモのブロックは2 x 2の四角の形ですが、上記データ構造は4 x 2のマスです。
テトリスでは、落ちるブロックの形は7種類あります。全部の形を定義するには 4 x 2 のマスが必要なのです。7種類のブロックの形の定義と、回転の処理は次回の記事に譲ります。
さて、ブロックが落ちていって、下の境界に触れたら止まります。これを判断するのには、ブロックの座標とブロックの形を表したデータが必要です。
ブロックが何かに当たったかどうかを判定するのに blockHit()関数を定義しています。この関数の中で、hasBrick() 関数を使って、screen ないの特定の位置のマスの中身を確かめています。
function blockHit(x, y, shape) {
// ブロックの形データ4 x 2を見ていく
for (j = 0; j < 2; j++) {
for (i = 0; i < 4; i++) {
if (shape[i+j*4]==1) {
if (hasBrick(x+i, y+j))
return true;
}
}
}
return false;
}
function hasBrick(x,y) {
return 0!=screen[x + y*SCREEN_W];
}hasBrick()関数では、screen の特定の位置のマスが0ではない、ということでブロックがあると判断しています。
ここは少々トリッキーなところですが、y が screenの下端のエリア外の場合も hasBrick()は true を返します。hasBrick()関数は、下端の範囲外になった場合も判断可能です。
10 x 20 のエリアに対しては、yは0〜19が範囲内です。 y が 20のときは配列の index を超えます。配列の範囲外に対してアクセスした場合は undefinedが返ります。結果、0 != undefined なので trueになるという訳です。
積み上げ処理
ブロックがそれ以上落下できない場合は、その場所に積み上がっていきます。この処理はupdate()関数の中で実装しています。
function update() {
・・・
if (blockHit(blockX, blockY+1, blockShape)) {
putBlock(blockX, blockY, blockShape); // ブロックを積み上げる
blockY = 0;
return;
}
・・・
}blockHit()関数で、一段下の場所に何かに当たった場合は、putBlock() 関数を呼んでいます。
putBlock()関数は以下の実装です。4 x 2のブロックの形にそって、screen バッファにデータをセットしています。
function putBlock(x, y, shape) {
// ブロックの形データ4 x 2を見ていく
for (j = 0; j < 2; j++) {
for (i = 0; i < 4; i++) {
if (shape[i+j*4]==1) {
setBrick(x+i, y+j, 1);
}
}
}
}
function setBrick(x, y, block) {
screen[x + y*SCREEN_W] = block;
}ラインを消す処理
これまで、ブロックが落ちていき何かにあたれば積み上がっていく処理を見てきました。
積み上がったブロックがあるかどうかは、screenバッファを見ればわかります。
ラインが揃っているかを見るのは簡単です。ある行がすべて 1 になっているのかを確認すれば良いのです。以下がその実装です。
function lineIsComplete(line) {
for (i = 0; i < SCREEN_W; i++) {
if (screen[i + line*SCREEN_W]==0)
return false;
}
return true;
}アルゴリズム的には、行の中のどれかの要素が0ならラインは揃っていない、を判断した方が効率が良いので、そういう実装になっています。
さて、ラインが揃ったらそのラインが丸ごと消えて、その後、上に積まれたブロックが落ちる。という動きをします。以下のその実装です。
function checkLineComplete() {
do {
deleted_line = false;
for (j = SCREEN_H-1; j >=0 ; j--) {
if (lineIsComplete(j)) {
deleteLine(j);
j++;
deleted_line = true;
}
}
} while (deleted_line);
}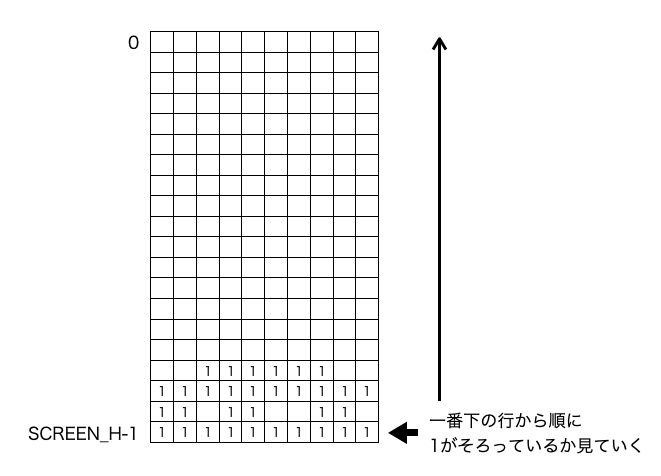
1が揃っている行を見つけたら、その行を削除して、上の行を下に詰めます。そこはdeleteLine()関数でやっています。
function deleteLine(line) {
for (j = line-1; j >= 0; j--) {
copyLine(j,j+1);
}
}
function copyLine(src, tgt) {
for (i = 0; i < SCREEN_W; i++) {
screen[i + tgt*SCREEN_W] = screen[i + src*SCREEN_W];
}
}deleteLine()でやっているのは、消したい行の上の行を自分にコピーすることです。これをずっと上まで辿っていきます。簡略化すると、やっていることは下記図に示している通りです。
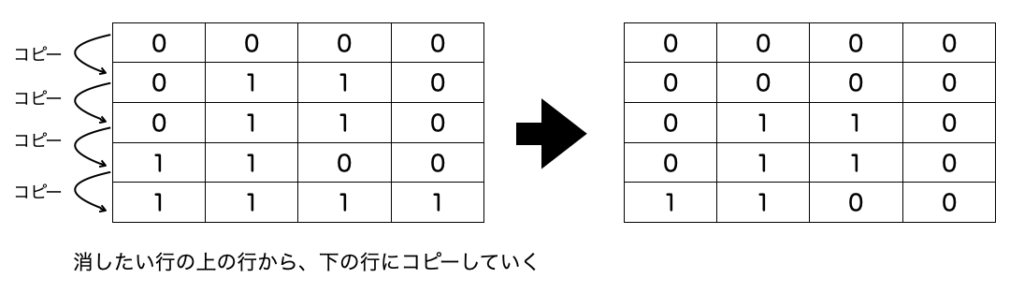
これを1が揃っているラインがなくなるまで繰り返します。
もっと効率の良いアルゴリズムも考えられますが、データ構造の単純さとのトレードオフもありますし、ひとまずこれで良しとします。
次回は
さて、テトリスのゲーム性を構成する基本要素のうち、以下のギミックを実装しました。
- ブロックが落ちる
- ブロックが積み上がる
- ラインいっぱいに積まれたら行が消える
あと残っているのは、ブロックの種類を増やすことと、ブロックを回転できるようにすること、くらいです。次回はこれらを実装して、ミニマムなテトリスの完成といきたいと思います。









